R 기초
*** R 기초 강의 내용을 정리한 글입니다.
==3.10==================================================
R 설치, 초기설정, 기초.
구글 검색 : R
English 버전으로 다운로드.
구글 검색 : Rstudio
IDE 다운로드 - Desktop 버전. free 다운로드
*가능하면 관리자 권한으로 설치하라
[Rstudio]
새 스크립트] new file → Rscript
초기 설정] tools → gobal option → code → editing -> soft-wrap R source files 체크
→ saving → change → utf-8로 변경
글씨 조정 기능] tools → gobal option → appearance
코드 실행] ctrl + Enter
코드 저장] ctrl + s
프로젝트 생성] 우측 상단 : project : none ⇒ new project ⇒ new directory ⇒ new project
⇒ 파일이름 : temp 생성
스크립트 저장] 스크립트 생성 ⇒ ctrl + s ⇒ 이름 : ch01 생성
라이브러리 설치] 구글 검색 : Rtools → using rtools on window → 64bit 버전 다운로드
→관리자 권한으로 install 실행. → 에러 발생 시) 단체 채팅 방 링크로 들어가 4번 영상을 참고.
→ 에러 발생 시) 원 드라이브 비활성화
*경로에 한글이 있어도 에러.
라이브러리 사용] 스크립트에 다음 내용을 복사 붙여넣기 → 실행 → 저장 → 종료write('PATH="${RTOOLS40_HOME}\\usr\\bin;${PATH}"', file = "~/.Renviron", append = TRUE)
→ temp 파일 켜기 → 스크립트에 다음 내용을 복사 붙여넣기Sys.which("make")
→ 실행 → console 창에 sys.which(”make”) 가 출력되면 성공.
→ 다음 내용을 복사 붙여넣기install.packages("jsonlite", type = "source")
→ 실행 → DONE (jsonlite) 출력 시 성공.
→ 다음 내용을 복사 붙여넣기install.packages("tidyverse")
install.packages(”ggplot2”)
→ 실행 → 다운로드 완료 → 다음 내용을 복사 붙여넣고 각각 실행
library(ggplot2)library(tidyverse)iris <- iris
→ console 창에 iris←iris 가 출력되면 성공.→ 다음 내용을 복사 붙여넣기
ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width)) + geom_point()
→ 실행 → 우측의 plot에 그림이 출력되면 성공
[GitHub]
gitHub 회원가입
구글 검색 : git → git download → window → 64bit 다운로드
시스템 환경 변수 편집 → 시스템 환경 변수 → 시스템 변수 : path → 편집 → cmd있는지 확인
다음 링크 → code → 복사
https://github.com/dschloe/R_edu
바탕화면 → 우클릭 → git bench here → git 창에 다음 내용 입력.
→ 바탕화면 : R_edu 파일 생성 시 성공
$ git clone https://github.com/dschloe/R_edu.git
(cd Desktop에서 설치가 진행되어야 한다.)
바탕화면 → R_edu 파일 → R_edu 실행
[패키지]
여러 함수를 모아놓은 것
- 패키지 설치 : install.packages(”패키지 이름”)
- 패키지 구동 : library(패키지 이름)
다음 링크 → packeges → 원하는 것을 찾아 사용.
The Comprehensive R Archive Network (r-project.org)
예시) ggplot2의 패키지 → packages에서 ctrl + F 로 검색. → 메뉴얼 읽고 사용.
*ggplot2는 R참고서 201p에 기재되어있다.
사용 예시) The Comprehensive R Archive Network (r-project.org) → packages → Table of available packages, sorted by date of publication → (원하는 패키지를 ctrl + F로 찾아서 선택) ggplot2 → reference manual : ggplot2.pdf 를 클릭 → (index에서 원하는 함수를 선택해 이동)
→ Example 항목을 찾아서 복사 → 스크립트에 붙여넣기 → 스크립트 맨 위에 install.packagese(함수 이름) 작성 → 실행 → 사용 가능.
다음 명령을 스크립트에서 실행
library(ggplot2)
install packages(”writexl”)
library(writexl)
library(ggplot2) // 다운 받은 것을 가져와서 사용한다는 의미
ggplot()
*이후에 R 심화 과정을 원할 경우 참고 : 원서 https://r4ds.had.co.nz/
그래프 시각화 지원 https://www.r-graph-gallery.com/
[그래프 시각화 지원 plot 사용 ]
Basic ridgeline plot – the R Graph Gallery (r-graph-gallery.com)
위 링크의 코드 복사 → 스크립트에 붙여넣기 → 실행.
[치트 시트]
자주 사용하는 것들을 모아놓은 것.
Rstudio → help → cheat sheets → browser cheat sheets 또는 data visualization with ggplot2
위 과정대로 진행 시 cheat seet가 다운로드 됨.
chapter 1. 기초 문법
1 / 100 * 30
a <- 1 / 100 * 30
b <- 1 / 1000
a <- “A그룹” # (x)
a <- “A그룹”
groupA <- “A그룹”
group_A <- “A그룹”
group.A <- “A그룹”
r_basics <- 3
r_basics
변수 유형 확인 예시
class(r_basics)
class(group_A)
temp <- TRUE
class(temp)
[3장 데이터 타입]
R을 이용한 공공데이터 분석 36p.
chapter 2.벡터 만들기
num_vector = c(1,2,3)
print(num_vector)
class(num_vector)
char_vector = c(“A”,”B”,”C”)
print(char_vector)
class(char_vector)
logical_vector = c(TRUE, FALSE, FALSE)
print(logical_vector)
class(logical_vector)
(1) 예외
temp = c(1, “1”, 2)
print(temp)
class(temp) // 모두 문자화
temp = c(1, FALSE, TRUE)
print(temp)
class(temp) // 모두 숫자화
temp = c(“A”,FALSE, TRUE)
print(temp)
class(temp) // 모두 문자화
####(2) 범주형 변수 ####
#비서열 척도 = 명목형 척도
location_vector = c(“서울”, “경기”,”대구”, “광주”)
fct_vector = factor(location_vector)
print(fct_vector)
class(fct_vector)
결과)
print(fct_vector)
[1] 서울 경기 대구 광주
Levels: 경기 광주 대구 서울
class(fct_vector)
[1] “factor”
#서열 척도
fct_vector2 = factor(location_vector,ordered=TRUE)
print(fct_vector2)
class(fct_vector2)
결과)
print(fct_vector2)
[1] 서울 경기 대구 광주
Levels: 경기 < 광주 < 대구 < 서울
class(fct_vector2)
[1] “ordered” “factor”
==3.11==================================================
dplyr 함수 사용하기 & 어떤 로컬에 있든 불러오기 & 시각화
install.packages(“패키지명”)
library(dplyr) # 데이터 가공
이름 <- c(“evan”, “윤석열”, “이재명”)
나이 <- c(20, 30, 40)
지각 <- c(TRUE, FALSE, FALSE)
students <- data.frame(name = 이름,
age = 나이,
atte = 지각)
str(students)
#경로확인
getwd()
#파일저장
write.csv(x = students, file = “학생.csv”)
#엑셀로 내보내기
install.packages(”writexl”)
library(writexl)
write_xlsx(x=student, path= ”학생.xlsx”)
#모두 지우기
rm(list=ls())
#파일 불러오기
getwd()
students <- read.csv(“학생.csv”)
****중요
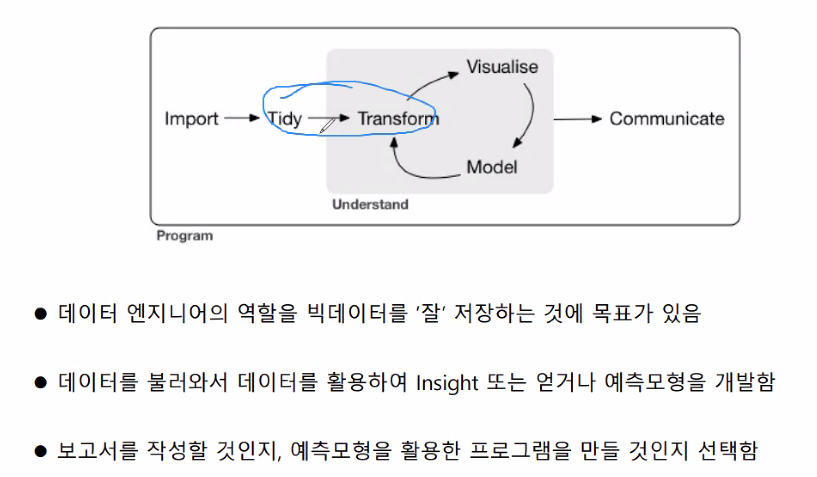
위 파란 부분이 가장 오래 걸리는 부분이다.
sql 문법과 유사하여, dplyr패키지를 배운 뒤,
sql을 배우면 보다 빠르게 쿼리 작성에 능숙해질 수 있음
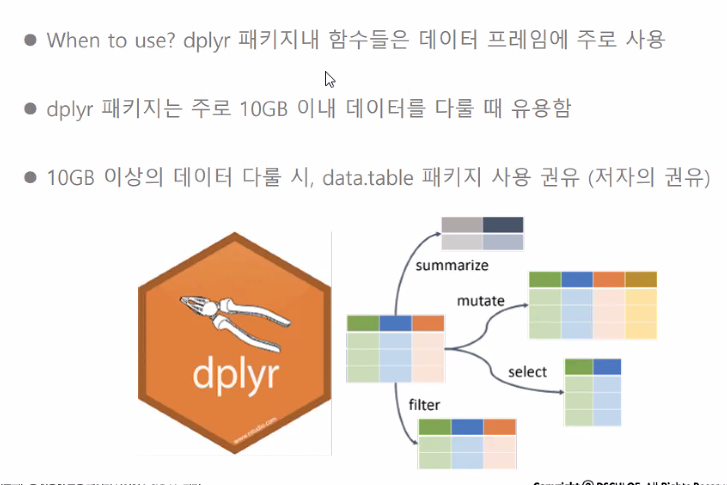
#dplyr 패키지
library(dplyr)
iris ← iris
str(iris)
iris %>% #~에서 # 150개, 5개의 변수
select(Sepal.Length, Sepal.width) %>% # 150개, 2개
filter(Sepal.Length > 6) %>% # 61개, 2개의 변수
..
..
head(10) → iris2 # 10개, 2개의 변수
?head()
구글 검색 : dplyr → 쿠라레? → 다음링크 → dplyr.pdf
CRAN - Package dplyr (r-project.org)
로우데이터=가공되지 않은 데이터
dplyr = 데이터 가공
과제: 교재 98p에서부터 명령어 하나씩 써보기
과제: 하루에 코딩 5,6 시간
강사님이 카톡으로 전송한 data, solution 파일 다운로드
r_edu 파일로 실행 → 다음과 같은 경로로 폴더를 연다 → 1_2_dplyr 실행.
위 그림에서 ‘(톱니바퀴 모양) more’→ set as working directory # 경로 잡기
1_2_dplyr 파일에서 다음 내용을 실행
counties <- readxl::read_xlsx(“counties.xslx”, sheet = 1).
만약 에러나오면
다음과 같이 data/ 를 추가하거나, read의 괄호안에서 Tab으로 찾아라.
counties <- readxl::read_xlsx(“data/counties.xslx”, sheet = 1)
[restats 파일 부르기]
다음을 실행.
getwd()
stats <- read.csv(“data/restats.csv””) # restats.csv
[파일 미리보기]
glimpse(counties) 실행 → 안되면, library(dplyr) 실행 후에 다시 실행.
강사님이 카톡으로 전송한 public dataset 파일 다음 경로에 다운로드
바탕화면 → solution → data → () 여기에 다운로드.
새스크립트 : dplyr_practice 만들고 1 or 2 선택해서 해보기
책 99p에 있는 코드부터 알아서 실행해보기.
구글 검색:r-4 data → 5 data transformation 참고해서 실행해보기
QnA) 교재 104p 참고 → :: 에 대한 질문.
불러올 때는 더블콜론(::)을 이용해서 불러오시오
install.packages(”hflights”)
library(hflights) # 불러와서 씀
hflights = hflights::hflights # 임시로 잠깐 씀
둘다 비슷한 기능.
[불러오는 법]
- 경로는 more → set as working directory 에서 잡고
- 위치는 read.csv(””) 에서 tab으로 찾아 들어가라.
불러오는 법 ex)
- more → set as working directory
- 다음 같은 형식으로 실행.
getwd()
student <- read.csv(“source_2021/1_day_eda/data/student.csv”)
mpg1 <- read.csv(“source_2021/1_day_eda/data/public_dataset/mpg1.csv”)
강사님이랑
1_2_dplyr 스크립트의 내용을 따라감.
glimpse , select, arrange, filter, mutate 등 배움.
count, summarise 등 배움.
summarise에 앞서 엑셀의 피벗테이블 개념 숙지.
피벗테이블 = 엑셀에서 시트의 일부분을 엮어 세팅하는 정보 테이블
다음을 참고.
엑셀 | 피벗 테이블(Pivot Table) 만드는 방법 – ㈜소프트이천 (soft2000.com)
group by 사용 예시
counties %>%
select(state, population, private_work, public_work, self_employed) %>%
group_by(state) %>%
summarise(min_pop = min(population),
max_pop = max(population),
avg_pop = mean(population))
[시각화]
수많은 데이터를 분석해야 하지만 한 눈에 들어오도록 하는 것은 쉽지 않다.
방대한 데이터를 한 눈에 보이게 만드는 것이 시각화이다.
시각적 요소를 이용해 대량의 데이터를 강제로 인지시킨다고 한다.
*참고)
구글검색 : inf learn → 시각화
구글검색 : dacon → 시각화 경진대회 & 참가자 제출물 참고하기.
구직자를 위한 기업 트렌드 시각화 경진대회 - DACON
구글검색 : the R graph 갤러리, 유니콘
https://exts.ggplot2.tidyverse.org/gallery/
깃허브 : 강사님 깃
https://github.com/IndrajeetPatil/ggstatsplot
[시각화 코딩]
바탕화면 → R_edu → 금융데이터사이언스 스킬업.pdf → p51 참고
ggplot(data = data, aes(x = x축, y = y축)) + geon_poinrt() + ylim(3,6)

코딩 예시)
library(ggplot2)
iris <- iris
str(iris)
ggplot(data = iris, aes(x = Sepal.Length, y = Sepal.Width)) + geom_abline() + 옵션
[시각화 저장]
위 코드 실행 → plot에 시각화 자료 출력. → export → save as image
→ directory → 바탕화면으로 설정 → save
팁
?명령어 → 실행 → 해당 명령어의 메뉴얼이 출력된다.
==3.14==================================================
시각화.
나이팅게일
-간호사, 통계학자
-전쟁 중 사고 나서, 총이나 칼, 포탄 → 통념) 죽는 사람 많을 거라 생각.(현장 모르는 분)
-위생&부상 → 실제) 죽는 사람이 훨씬 많음(현장을 아는 분)
-제안 : 위생 강화 & 야전 병원을 좀 더 짓자 → 설득 : 그래프를 이용한 시각적 통계
시각화 표 : “금융데이터사이언스 스킬업.pdf” 53p 참고.
[시각화 실습]
질병 관련 통계.
temp 프로젝트 오픈. → 새 스크립트 → 0314.R 만들기.
바탕화면 → data → who_disease 불러와서 사용 .
데이터 불러오기
library(dplyr)
library(ggplot2)
library(readxl)
who_disease <- read_xlsx(“who_disease.xlsx”)
iris <- iris
glimpse(iris)
데이터 확인
glimpse(who_disease)
산점도 그려보기(의미없음)
ggplot(who_disease, aes(x=year,y=cases)) +
geom_point()
투명도 주기
ggplot(who_disease, aes(x=year,y=cases)) +
geom_point(alpha=0.3)
투명도,색 주기
ggplot(who_disease, aes(x=year,y=cases)) +
geom_point(alpha=0.3, colour = “red”, size=10)
그룹화
ggplot(who_disease, aes(x=year,y=cases,
colour=region))+
geom_point()
0314.R 에 다음 내용 복사 붙여 넣기.
R_edu → … → solution → 1_3_ggplot 의 ( 64 line~끝 line ) 까지 긁어서 실습.
install.packages(”waffle”)
install.packages(“carData”)
install.packages(“ggpol”)
install.packages(“ggcorrplot”)
install.packages(“mosaicData”)
install.packages(“visreg”)
install.packages(“gapminder”)
install.packages(“ggpubr”)
install.packages(“ggthemes”)
install.packages(“nycflights13”)
install.packages(“reshape”)
#install.packages(“gcookbook”)
install.packages(“ggthemes”)
*팁 : 구글 검색
- 영어로 검색하라.
- how to code 또는 how to write로 시작하라.
ex) how to write yaxis dollar sign ggplot2
[시각화 실습]
R_edu → … → solution → 1_4_ggplot 실습.
[옵션 이용하기]
*367p 참고
*메뉴얼 참고
R Markdown: The Definitive Guide (bookdown.org)
Rstudio → File 아래 (+)마크 클릭 → R Markdown
→ title, author 작성하고 OK → 생성됨 → 작명:report로 저장 → .rmd 확장자로 저장됨.
→ 톱니모양 옆에 ‘knit’ 클릭 → 관련 정보가 출력된다.

R Markdown 언어 작성 → (+)마트 달린 ‘c’ 아이콘을 클릭 → R 선택
→ R 작성 가능 창이 출력됨 → 입력 후 실행 → knit에 반영됨.
다음과 같은 식으로 report.Rmd에 적고 knit을 출력해보아라.
웹에서도 knit을 확인할 수 있다.
knit은 desktop→data→report.html 클릭→ view in web
*팁
아래의 R작성 가능 창에 install.packages를 올리지 말고 따로 install만 해놓면
library만 작성해도 잘 돌아간다.
4. 데이터 전처리
1) 분석파일을 R로 불러오기
1 | library(dplyr) |
2) 시각화 코드
- 데이터를 불러와서 Sepal.Length, Sepal.Width 두 변수에 관한 산점도 시각화를 작성한다.
1 | ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width)) + |
[배포]
knit 출력 → 우측 상단의 ‘publish’ → Rpubs (무료버전) → publish
→create an account → 내용을 임의로 작성하고 ‘continue’ → 주소를 복사해 카톡으로 전송
→본인 핸드폰으로 접속해본다. → 성공 시 knit 내용이 반영된 페이지에 접속됨.
→ 배포 : 페이지 게시 완료
[시각화 실습]
R_edu → … → solution → 1_5_ggplot 실습. → 125 line ~ end of document
구글링 : ggplot extensions → 마음에 드는 테마를 적용 가능.
→ 테마 이름을 참고하여 다운로드 ex) install.packages(“ggthemes”)
→ 사용 예시를 보고 사용 ex) p + theme_stata()
[시각화 실습]
R_edu → … → solution → 1_6_ggplot 실습 → 폰트 적용 연습
[R 참고서적]
추가적인 공부를 원할 때 참고하라.
-R data visualization
-데이터 시각화 교과서
-R을 활용한 데이터 시각화
==3.15==================================================
통계.
[데이터 분석]
-데이터수집
-데이터가공
-데이터시각화
-모델링 : 통계 모델링 / 머신러닝 모델링 / 딥러닝 모델링
-통계를 도대체 어디까지 알아야 하나?
-선형대수를 얼마나 알아야 하나?
-Top-Down방식 / Bottom-up방식
-모델링과 관련된 수식을 얼마나 알아야 하나?
[진로와 관련]
: 웹 개발자 → 라이브러리 자 갔다 쓰고, 배포 잘하면 끝.
: 데이터 분석가 → 마케터(기획) / 여론조사
-기본적인 통계(고재 8장 통계 분석)
-모수 검정 / 비모수 검정 —> 빈도 주의
-베이지안
: 머신러닝 엔지니어 / 딥러닝 엔지니어
-통계 / 선형대수 필요 / 모델링 수식 굳이…
-모형 만들고 배포를 잘해야 함(개발자)
-포폴 : 머신러닝 논문 정리(최신)
-라이브러리로 이미 만들어져 있음
-구글링 : paperswithcode → 딥러닝 관련내역
: 머신러닝 / 리서쳐 알고리즘 직접 구현
-최소 석사(관련 논문)
-네이버,카카오AI
-라이브러리를 직접 만드시는 분들
:Top-down 방식
-분석의 방향(수치 예측/분류 위주 예측)
-그룹간의 비교/인과관계
-산업분야
[ 기초 통계 ]
참고
temp → 2_day_stat_reggression → data → 기초 통계-평균,중간값,분산,표준편차.pdf

deviation: 편차
x1 : 개별 관찰값
x : 평균

vlariance : 분산 (= 편차 제곱의 평균)
x1: 개별 관찰값
x : 평균
분산값이 크다 —> 평균으로부터 멀어진 개별적인 데이터가 많다. = 흩어져있다.
분산값이 작다 —> 평균주위에 개별적인 데이터가 많다. = 평균쪽에 몰려있다.
즉, 분산은 평균으로부터 떨어진 거리를 나타냄.
모집단과 분산

*참고
temp → 2_day_stat_reggression → data → 기초 통계-변동계수.pdf

CV= 변동계수
RSD= 상대 표준 편차
평균 : u
표준편차 : o
install.packages(“tidyquant”)
install.packages(“reshape2”)
*참고
temp → 2_day_stat_reggression → data → 기초 통계-사분위수.pdf
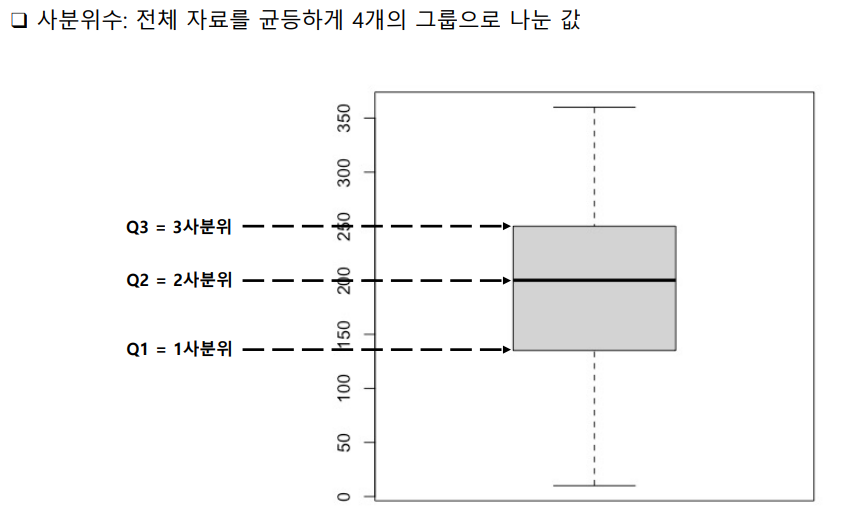
이상치 판별: 중심에서 많이 떨어진 값을 의미
이상치 하한 Q1 - 1.5x(Q3-Q1)
이상치 상한 Q3 + 1.5x(Q3-Q1)
[통계 실습]
슬랙 → #edu 채널 → 3/15에 게시된 ‘3교시 코드’ 참고
*참고
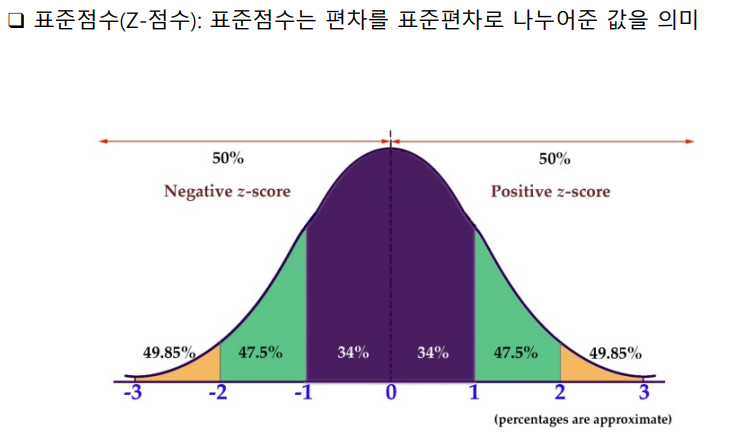
temp → 2_day_stat_reggression → data → 기초통계-z_score.pdf

X = 원 데이터
M = 평균
SD = 표준편차
*참고
temp → 2_day_stat_reggression → data → 기초통계-z_test.pdf
❑ 가설검정(Hypothesis Testing)
-평균에 대한 가설 검정
-잘못된 가정: 대한민국 성인의 키는 크다
-올바른 가정: 대한민국 성인의 평균 키는 170cm 이다 .
❑귀무가설 및 대립가설
o 귀무가설(H0)
-내용: 대한민국 성인의 평균 키는 170cm이다.
-통계적 표시법: H0: u = 170
o 대립가설(H1)
- 내용
• 평균 키는 170이 아니다. = 제1형 = 양측검정
• 평균 키는 170보다 작다. = 제2형 = 단측검정 = 좌측 검정
• 평균 키는 170보다 크다. = 제3형 = 단측검정 = 우측 검정
❑ 가설 선택의 기준 수립
1종 오류(type 1 error)
→ 제1종 오류는 우리가 모집단에 효과가 진짜로 존재한다고 믿지만
사실은 아무런 효과도 없는 것이다.
2종 오류(type 2 error)
→ 제1종 오류와는 반대이다. 즉, 모집단에 실제로 효과가 존재하지만
우리는 모집단에 아무 효과도 존재하지 않는다고 믿는 것이 제2종 오류이다.
o 유의수준
- 제 1종 오류를 범할 확률의 최대 허용 한계 (유의수준 a)
표는 z_test.pdf 참고.
[통계 실습]
temp → 2_day_stat_reggression → source → 2_5_1_hypothesis_testing.R
temp → 2_day_stat_reggression → source → 2_5_2_one_sample.R
temp → 2_day_stat_reggression → source → 2_5_3_paired_t_test.R
*참고
temp → 2_day_stat_reggression → data → 기초통계-???
두 평균의 비교 (대응 표본 vs 독립표본)
단일 표본 T-Test
- 차이가 있는가? (모집단 vs 표본)
두개 표본 T-Test
대응표본 예시 : 신약 개발 시험 (사전 테스트 + 사후 테스트)
독립표본 예시 : 남자와 여자의 몸무게 비교
공통 사항 검정
- 정규성 검정 여부 확인
데이터 T-Test는 정규성 여부 확인을 전제로 만들어져서
단일 모집단 검정시에도 정규성 여부 조건을 확인해야 한다.
ex) 레벨이 부족할 때 고레벨 전용 아이템을 사용 못하는 것과 같다.
==3.16==================================================
R의 마지막
[전날 수업 내용 정리]
기초통계의 핵심 : 평균
편차 : 평균과 개별적인 데이터 사이의 거리
분사(variance) : 편차의 제곱합의 데이터 객수만큼 나눔
표준편차 : 분산에 루트 씌운다
표준편차 + 평균 활용
변동계수, z-score, 검정값, 표준오차
모수 검정
핵심: 두 그룹간의 평균의 차이를 검정
두 그룹간의 차이가 유의미하냐? 우연히, 어쩌다가 한 번 일어난거냐!
가정 : 데이터가 정규분표를 이룬다!
평균 비교
One Sample T Test : 모집단의 평균 ~ 샘플(표본)의 평균
대응표본 : 사전 표본의 평균(정책, 신약 투여 등등 시간이 지난 후) 사후 표본의 평균
독립표본 : A 그룹과 B그룹간의 평균 비교
결국은 평균을 비교하는 것.
귀무가설 ~ 대립가설
귀무가설 : 두 그룹가의 00평균의 차이가 없다!
대립가설 : 두 그룹간의 평균의 차이는 존재하더라!
t 통계량 / p-value
구글링 : 표준정규분포표 → 표를 보고 p-value값을 계산하면 된다
*팁
‘우리 나라 석사 학위 논문’
구글링 : RISS 하여 들어가서 찾아서 보면 된다.
논문은 별거 아니다.
다만, 데이터 수집하는 것이 가장 어렵다.
[기초통계-분산분석]
*참고
temp → 2_day_stat_reggression → data → 기초통계-분산분석.pdf
예를들어, 어느 학교의 3개의 반의 성적을 비교한다고 할 때, 3번을 비교해야한다.
분산분석
: 두 개 이상 다수의 집단을 서로 평균에서 분산값을 비교하기 위한 가설검정 방법
F분표
: 분산의 비교를 통해 얻어진 분표비율
계산식

-1학년 전체 학생 인원의 분산 : 300명 ( 분산=100) // 표본 내 분산
-각 반의 분산 // 표본 평균 간 분산
1반의 분산 90
2반의 분산 70
.
.
가설수립
-귀무가설 : 3학년 1,2,3반의 평균은 모두 같다.
-대립가설: 적어도 1개반의 평균은 다르다.
F통계량 공식
-F = 검정통계량
-F통계량은 오차의 평균제곱합과 처리의 평균제곱합의 비인 MST/MSE
-이를 나타내는 두 개의 자요도(k-1, n-k)를 모수로 하는 F-분포를 따르는 F 통계량
F = MST/MSE~F(k-1,m-k)
-MSE(오차 평균 제곱합) : 처리’내’ 제곱합을 자유도로 나눈 값
-MST(처리 평균 제곱합) : 처리’간’ 제곱합을 자유도로 나눈 값
일원분산분석 모형
검정통계량 구하기
-분산 : 각 개별 자료값과 평균과의 차이
-총편차 : 개별자료와 전체 평균(y)과의 차
- 총 제곱합 (SST) = 오차제곱합(SSE) + 처리제곱합(SST)
[통계 실습]
temp → 0314 스크립트 생성
분산분석
라이브러리 불러오기
library(dplyr)
library(ggplot2)
데이터 수집 및 가공
my_data = PlantGrowth
my_data$group <- ordered(my_data$group, levels=c(“ctrl”,”trt1”,”trt2”))
my_data %>%
group_by(group) %>%
summarise(
count = n(),
mean = mean(weight, na.rm= TRUE),
sd = sd(weight, na.rm = TRUE)
)
ggplot(my_data, aes(x=group, y=weight))+
geom_boxplot()
one=way ANOVA 테스트
오차제곱합(SSE)
ctrl <- my_data$weight[my_data$group==”ctrl”]
trt1 <- my_data$weight[my_data$group==”trt1”]
trt2 <- my_data$weight[my_data$group==”trt2”]
ctrl_mean = mean(ctrl)
trt1_mean = mean(trt1)
trt2_mean = mean(trt2)
각 처리별 제곱합
ctrl_sse = sum((ctrl-ctrl_mean)^2)
trt1_sse = sum((trt1-trt1_mean)^2)
trt2_sse = sum((trt2-trt2_mean)^2)
오차의 제곱합
sse <- ctrl_sse + trt1_sse + trt2_sse
sse
오차의 자유도
dfe <- (length(ctrl)-1) + (length(trt1)-1) + (length(trt2)-1)
처리의 제곱합 구하기 (SST)
total_mean = mean(my_data$weight)
ctrl_sst = length(ctrl) * sum((ctrl_mean - total_mean) ^ 2)
trt1_sst = length(trt1) * sum((trt1_mean - total_mean) ^ 2)
trt2_sst = length(trt2) * sum((trt2_mean - total_mean) ^ 2)
처리 제곱합
sst = ctrl_sst + trt1_sst + trt2_sst
처리 제곱합의 자유도
dft = length(levels(my_data$group)) - 1
전체 제곱합과 분해된 제곱합의 합 구하기
tsq = sum((my_data$weight - total_mean) ^ 2)
ss = sst + sse #총 제곱합
all.equal(tsq, ss) # TRUE
검정 통계량
mst = sst / dft
mse = sse / dfe
f.t = mst / mse
f.t
alpha = 0.5
tol <- qf(1-alpha, 2, 27)
tol
p.value = 1-pf(f.t, 2, 27)
p.value # 0.0159…
즉, 적어도 반 하나의 평균은 다르다.
위의 모든 과정을 아래의 코드로 축약 가능
res.aov <- aov(weight ~ group, data =my_data)
summary(res.aov) # p-value = 0.0159…
회귀식의 기본 공식
*참고
바탕화면 → R-edu → 금융데이터사이언스 스킬업.pdf → 101p 참고
회귀 : 이전 데이터를 바탕으로 앞으로의 일을 예상하는 것
예시) 날씨 & 온도 에 따른 아이스 아메리카노 판매량
온도, 강우, 위치 —> 설명변수, 독립변수
판매량 —> 종속변수, 반응변수
결과i = (model) + 오차i
model = 최소제곱법
model = 기울기 * 예측변수의 점수 + 절편 # 절편 = 기본으로(최소한도) 팔리는 아아 판매량
결정 계수( R-squared)
: 회귀모델의 추정된 회귀식이 관측된 데이터를 설명하고 있는 비율을 계수로 나타낸 것
: R 교재 186p 참고
팁
구글링 : wikidocs → Must learning With R (개정판) = e-book → 통계 관련 내용 참고
Must Learning with R (개정판) - WikiDocs
스캔파일 → 앤디 필드의 유쾌한 R 통계학 → 머신러닝 있어서 어려움 & 에러도 섞여있을 것.
유쾌한 알 통계학.pdf - OneDrive (live.com) 강의실 pc에 다운로드 완료
- Reference : R을 이용한 공공데이터 분석