지도학습과 비지도 학습

• 지도학습 : 경진대외 유형

• 입력과 타깃 : 독립변수(입력), 종속변수(타깃)

• 정답이 있는 문제

  • 1 유형 : 타이타닉 생존자 분류 : survived (타깃)
  • 2 유형 : 카페 예상매출액 : 숫자를 예측

• 특성(Feature) : 독립변수(엑셀의 컬럼)

• 비지도 학습 : 뉴스기사 종류를 분류

  • 기사 1 : 사회, 의학, …
  • 기사 2 : 사회, 경제, …

• 훈련 세트와 테스트 세트

1
2
3
4
5
6
7
8

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 
                10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 
                7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

1
2
3
4
5
6
7

fish_data = [[l,w] for l, w in zip(fish_length, fish_weight)]
# fish_data

# 1은 도미
# 0는 빙어
fish_target = [1]*35 + [0]*14
#fish_target

• 머신러닝 모델

1
2

from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()

훈련세트와 테스트 세트로 분리

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 0부터 ~ 34인덱스까지 사용
# 훈련데이터 독립변수
train_input = fish_data[:35]

# 훈련데이터 종속변수
train_target = fish_target[:35]

# 테스트데이터 독립변수
test_input = fish_data[35:]

# 테스트데이터 종속변수
test_target = fish_target[35:]

#train_input.shape, train_target.shape, test_input.shape, test_target.shape

1
2

kn = kn.fit(train_input, train_target)
kn.score(test_input, test_target)

0.0

1

fish_data[:34]

[[25.4, 242.0],
 [26.3, 290.0],
 [26.5, 340.0],
 [29.0, 363.0],
 [29.0, 430.0],
 [29.7, 450.0],
 [29.7, 500.0],
 [30.0, 390.0],
 [30.0, 450.0],
 [30.7, 500.0],
 [31.0, 475.0],
 [31.0, 500.0],
 [31.5, 500.0],
 [32.0, 340.0],
 [32.0, 600.0],
 [32.0, 600.0],
 [33.0, 700.0],
 [33.0, 700.0],
 [33.5, 610.0],
 [33.5, 650.0],
 [34.0, 575.0],
 [34.0, 685.0],
 [34.5, 620.0],
 [35.0, 680.0],
 [35.0, 700.0],
 [35.0, 725.0],
 [35.0, 720.0],
 [36.0, 714.0],
 [36.0, 850.0],
 [37.0, 1000.0],
 [38.5, 920.0],
 [38.5, 955.0],
 [39.5, 925.0],
 [41.0, 975.0]]

1

fish_target[34:]

[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

샘플링 편향

넘파이

• 리스트로 연산은 지원이 잘 안 됨.
• 리스트를 넘파이 배열로 변환

1
2
3
4
5
6

import numpy as np

input_arr = np.array(fish_data)
target_arr = np.array(fish_target)

print(input_arr.shape, target_arr.shape)    # shape 출력

(49, 2) (49,)

• suffle : 데이터를 섞어준다
• 실험 재현성
• np.random.seed(42) 란?
  • 뒤에 42는 무의미한 수치이다.
  • 랜덤 시드이다.
  • 어떤 특정한 시작 숫자를 정해 주면 컴퓨터가 정해진 알고리즘에 의해 마치 난수처럼 보이는 수열을 생성한다.
  • 이런 시작 숫자를 시드(seed)라고 한다.

1
2
3
4
5

# 76p
# 랜덤 시드
np.random.seed(42)
index = np.arange(49)
index

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
       34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48])

• 셔플

1
2
3

# 셔플 = 섞는다
np.random.shuffle(index)
print(index)

[13 45 47 44 17 27 26 25 31 19 12  4 34  8  3  6 40 41 46 15  9 16 24 33
 30  0 43 32  5 29 11 36  1 21  2 37 35 23 39 10 22 18 48 20  7 42 14 28
 38]

• 훈련 데이터 및 테스트데이터 재 코딩

1
2
3
4

train_input = input_arr[index[:35]]
train_target = target_arr[index[:35]]

print(input_arr[13], train_input[0])

[ 32. 340.] [ 32. 340.]

1
2

test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]

1

train_input.shape, train_target.shape, test_input.shape, test_target.shape

((35, 2), (35,), (14, 2), (14,))

시각화 생략

두 번째 머신러닝 프로그램

1
2

kn = kn.fit(train_input, train_target)
kn.score(test_input, test_target)

1.0

• 다음 두 코드의 결과가 같다. 예측 성공.

1

kn.predict(test_input)

array([0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0])

1

test_target

array([0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0])

02-2 데이터 전처리

넘파이로 데이터 준비하기

• 다음 주소를 참고하라 : bit.ly/bream_smelt

1
2
3
4
5
6
7
8

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 
                10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 
                7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

• 2차원 리스트를 작성해보자.
• 넘파이의 column_stack() 함수는 전달받은 리스트를 일렬로 세운 다음 차례대로 나란히 연결한다.

1
2
3

import numpy as np

np.column_stack(([1,2,3], [4,5,6]))

array([[1, 4],
       [2, 5],
       [3, 6]])

• 이제 fish_length와 fish_weight를 합친다.

1
2
3

fish_data = np.column_stack((fish_length, fish_weight))

print(fish_data[:5])

[[ 25.4 242. ]
 [ 26.3 290. ]
 [ 26.5 340. ]
 [ 29.  363. ]
 [ 29.  430. ]]

• 동일한 방법으로 타깃 데이터도 만들어 보자.
• np.ones()와 np.zeros() 함수를 이용한다.

1

print(np.ones(5))

[1. 1. 1. 1. 1.]

• np.concatenate() 함수를 사용하여 첫 번째 차원을 따라 배열을 연결해보자.

1
2
3

fish_target = np.concatenate((np.ones(35), np.zeros(14)))

print(fish_target)

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0.]

사이킷런으로 훈련 세트와 테스트 세트 나누기

• train_test_split()
  • 이 함수는 전달되는 리스트나 배열을 비율에 맞게 훈련 세트와 테스트 세트로 나누어 준다.
  • 사용법 : 나누고 싶은 리스트나 배열을 원하는 만큼 전달하면 된다.

1
2
3

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, random_state=42)

• fish_data와 fish_target 2개의 배열을 전달했으므로 2개씩 나뉘어 총 4개의 배열이 반환된다.
• 차례대로 처음 2개는 입력 데이터(train_input, test_input), 나머지 2개는 타깃 데이터(train_target, test_target)이다.
• 랜덤 시드(random_state)는 42로 지정했다.

1

print(train_input.shape, test_input.shape)

(36, 2) (13, 2)

1

print(train_target.shape, test_target.shape)

(36,) (13,)

• 훈련 데이터와 테스트 데이터를 각각 36개와 13개로 나누었다.
• 입력 데이터는 2개의 열이 있는 2차원 배열이고 타깃 데이터는 1차원 배열이다.
• 도미와 빙어가 잘 섞였는지 확인해보자.

1

print(test_target)

[1. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

• 13개의 테스트 세트 중에 10개가 도미(1)이고, 3개가 빙어(0)이다.
• 빙어의 비율이 좀 모자란데, 이는 샘플링 편항때문이다.
• 이러한 문제를 train_test_split() 함수로 해결할 수 있다.
• stratify 매개변수에 타깃 데이터를 전달하면 클래스 비율에 맞게 데이터를 나누다.
• 훈련 데이터가 작거나 특정 클래스의 샘플 개수가 적을 때 특히 유용하다.

1
2
3

train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, stratify=fish_target, random_state=42)

print(test_target)

[0. 0. 1. 0. 1. 0. 1. 1. 1. 1. 1. 1. 1.]

• 빙어가 하나 늘었다.
• 이전과 달리 비율이 좀 더 비슷해졌다.
• 데이터 준비가 완료되었다.

수상한 도미 한 마리

• 앞서 준비한 데이터로 k-최근접 이웃을 훈련해 보자.

1
2
3
4
5

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)

1.0

• 완벽한 결과이다. 테스트 세트의 도미와 빙어를 모두 올바르게 분류했다.
• 이 모델에 문제가 되었던 도미 데이터를 넣고 결과를 확인해본다.

1

print(kn.predict([[25, 150]]))

[0.]

• 도미 데이터인데 빙어로 나왔다.
• 산점도로 다시 확인해보자.

1
2
3
4
5
6

import matplotlib.pyplot as plt
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')  # marker 매개변수는 모양을 지정한다. '^'는 삼각형.
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

• 새로운 샘플은 marker 매개변수를 이용하여 삼각형으로 표시했다.
• 샘플은 오른쪽의 도미와 가까운 위치에 있는데 어째서 빙어로 판단했을까?
• k-최근접 이웃은 주변의 샘플 중에서 다수인 클래스를 예측으로 사용한다.
• KNeighborsClassifier클래스는 주어진 샘플에서 가장 가까운 이웃을 찾아 주는 kneighbors() 메서드를 제공한다.
  • 이 클래스의 이웃 개수인 n-neighbors의 기본값은 5이므로 5개의 이웃이 반환된다.

1

distances, indexes = kn.kneighbors([[25, 150]])

• indexes 배열을 사용해 훈련 데이터 중에서 이웃 샘플을 따로 구분해 그려본다.

1
2
3
4
5

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')   # 'D' 는 마름모 모양으로 출력
plt.xlabel('length')
plt.ylabel('weight')

Text(0, 0.5, 'weight')

• marker=’D’로 지정하면 산점도를 마름모로 그린다.
• 삼각형 샘플에 가장 가까운 5개의 샘플이 초록 다이아몬드로 표시되었다.
• 가장 가까운 이웃에 도미가 하나밖에 포함되지 않았다.

1

print(train_input[indexes])

[[[ 25.4 242. ]
  [ 15.   19.9]
  [ 14.3  19.7]
  [ 13.   12.2]
  [ 12.2  12.2]]]

• 가장 가까운 생선 4개는 빙어(0)인 것 같다.
• 타깃 데이터로 확인하면 더 명확하다.

1

print(train_target[indexes])

[[1. 0. 0. 0. 0.]]

• 해당 문제 해결의 실마리를 위해 distance배열을 출력해본다.
• 이 배열에는 이웃 샘플까지의 거리가 담겨 있다.

1

print(distances)

[[ 92.00086956 130.48375378 130.73859415 138.32150953 138.39320793]]

기준을 맞춰라

• 산점도를 다시 살펴본다.
• 삼각형 샘플과 근처 5개 샘플 사이의 거리가 이상하다.
• 가장 가까운 것과의 거리가 92이고, 그 나머지는 두 배 이상 멀어보이는데 수치는 그렇지 않다.
• 이는 x의 범위가 좁고 y축의 범위가 넓기에 그렇게 보이는 것이다.
• 명확하게 보기 위해 x축의 범위를 동일하게 맞춘다.
  • xlim()함수를 사용하여 x축 범위를 지정한다.

1
2
3
4
5
6
7

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000)) # x축 지정
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

• 두 특성(길이와 무게)의 값이 놓인 범위가 매우 다르다.
• 이를 투 특성의 스케일(scale)이 다르다고 한다.

데이터 전처리

• 데이터를 표현하는 기준이 다르면 알고리즘이 올바르게 예측할 수 없다.

• 알고리즘이 거리 기반일 때 특히 그렇다. 여기에는 k-최근접 이웃도 포함된다.

• 이런 알고리즘들은 샘플 간의 거리에 영향을 많이 받으므로 제대로 사요하려면 특성값을 일정한 기준으로 맞춰 주어야 한다.

• 이런 작업을 데이터 전처리(data preprocessing)이라고 부른다.

• 표준 점수

  • 가장 널리 사용하는 전처리 방법 중 하나는 표준점수(standatd score)이다.
  • 표준점수는 각 특성값이 평균에서 표준편차의 몇 배만큼 떨어져 있는지를 나타낸다.
  • 이를 통해 실제 특성값의 크기와 상광없이 동일한 조건으로 비교할 수 있다

1
2

mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)

• np.mean() 함수는 평균을 계산하고, np.std() 함수는 표준편차를 계산한다.
• axis=0으로 지정했으며, 이렇게 하면 행을 따라 각 열의 통계 값을 계산한다.

1

print(mean, std)

[ 27.29722222 454.09722222] [  9.98244253 323.29893931]

• 각 특성마다 평균과 표준편차가 구해졌다.
• 이제 원본 데이터에서 평균을 빼고 표준편차로 나누어 표준점수로 변환한다.

1

train_scaled = (train_input - mean) / std

• 브로드 캐스팅 (breadcastion)
  • 이 식은 어떻게 계산될까?
  • 넘파이는 train_input의 모든 행에서 mean에 있는 두 평균값을 뺀다.
  • 그 다은 std에 있는 두 표준편차를 모든 행에 적용한다.
  • 이런 넘파이 기능을 브로드캐스팅이라고 부른다.

전처리 데이터로 모델 훈련하기

• 앞에서 표준점수로 변환한 train_scaled를 만들었다.
• 다시 샘플을 산점도로 그려보자.

1
2
3
4
5

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

• 우측 상단에 샘플 하나가 덩그러니 떨어져 있다.
• 훈련 세트를 mean(평균)으로 빼고 std(표준편차)로 나누어 주었기 때문에 값의 범위가 달라졌다.
• 동일한 기준으로 샘플을 변환하고 다시 산점도를 그려보자.

1
2
3
4
5
6

new = ([25, 150] - mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

• 훈련 데이터의 두 특성이 비슷한 범위를 차지하고 있다.
• 이제 이 데이터셋으로 k-최근접 이웃 모델을 다시 훈련해 보자.

1

kn.fit(train_scaled, train_target)

KNeighborsClassifier()

• 테스트 세트의 스케일을 변환해 보자.

1

test_scaled = (test_input - mean) / std

• 이제 모델을 평가한다.

1

kn.score(test_scaled, test_target)

1.0

• 완벽하다. 모든 테스트 세트의 샘플을 완벽하게 분류했다.
• 앞서 훈련 세트의 평균고 표준편차로 변환한 김 팀장의 샘플 사용해 모델의 예측을 출력해보자.

1

print(kn.predict([new]))

[1.]

• 드디어 도미(1)로 예측했다. 확일시 길이가 25cm이고 무게가 150g인 생선은 도미일 것이다.
• 마지막으로 keighbors()함수로 이 샘플의 k-최근점 이웃을 구한 다음 산점도로 그려보자.
• 특성을 표준점수로 바꾸었기 때문에 알고리즘이 올바르게 거리를 측정했을 것이다.

1
2
3
4
5
6
7

distances, indexes = kn.kneighbors([new])
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes,0], train_scaled[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

• 삼각형 샘플에서 가장 가까운 샘플은 모두 도미이다.
• 따라서 이 수상한 샘플을 도미로 예측하는 것이 당연하다.
• 성공이다. 특성값의 스케일에 민감하지 않고 안정적인 예측을 할 수 있는 모델을 만들었다.

전체 소스 코드

• 다음 주소를 참고하라 : bit.ly/hg-02-2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 
                10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 
                7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

import numpy as np

np.column_stack(([1,2,3], [4,5,6]))

fish_data = np.column_stack((fish_length, fish_weight))
print(fish_data[:5])
print(np.ones(5))

fish_target = np.concatenate((np.ones(35), np.zeros(14)))
print(fish_target)

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
    fish_data, fish_target, random_state=42)
print(train_input.shape, test_input.shape)
print(train_target.shape, test_target.shape)
print(test_target)

train_input, test_input, train_target, test_target = train_test_split(
    fish_data, fish_target, stratify=fish_target, random_state=42)
print(test_target)

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)

print(kn.predict([[25, 150]]))

import matplotlib.pyplot as plt

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

distances, indexes = kn.kneighbors([[25, 150]])

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

print(train_input[indexes])
print(train_target[indexes])
print(distances)

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)

print(mean, std)

train_scaled = (train_input - mean) / std

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

new = ([25, 150] - mean) / std

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

kn.fit(train_scaled, train_target)

test_scaled = (test_input - mean) / std

kn.score(test_scaled, test_target)

print(kn.predict([new]))

distances, indexes = kn.kneighbors([new])

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes,0], train_scaled[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

[[ 25.4 242. ]
 [ 26.3 290. ]
 [ 26.5 340. ]
 [ 29.  363. ]
 [ 29.  430. ]]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0.]
(36, 2) (13, 2)
(36,) (13,)
[1. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[0. 0. 1. 0. 1. 0. 1. 1. 1. 1. 1. 1. 1.]
[0.]

[[[ 25.4 242. ]
  [ 15.   19.9]
  [ 14.3  19.7]
  [ 13.   12.2]
  [ 12.2  12.2]]]
[[1. 0. 0. 0. 0.]]
[[ 92.00086956 130.48375378 130.73859415 138.32150953 138.39320793]]

[ 27.29722222 454.09722222] [  9.98244253 323.29893931]

[1.]

• Reference : 혼자 공부하는 머신러닝 + 딥러닝

혼자 공부하는 머신 러닝 + 딥러닝

생선 분류 문제

• 한빛 마켓에서 팔기 시작한 생선은 ‘도미’, 곤들매기’, ‘농어’, ‘강꼬치고기’, ‘로치’, ‘빙어’, ‘송어’이다.
• 이 생선들을 프로그램으로 분류한다고 가정해 보자. 어떻게 프로그램을 만들어야 할까.

도미 데이터 준비하기

• 우선 생선의 특징을 알기 쉽게 구분해보자.
• 예를들어 30cm이상인 생선은 도미라고 한다.

1
2

#if fish_length >= 30:
#  print("도미")

• 하지만 이는 절대적인 기준이 될 수 없다.
• 기준을 제대로 파악하기 위한 과정을 수행해보자.
• 데이터는 다음 링크를 참고하라.: https://gist.github.com/rickiepark/b37d04a95a42ef6757e4a99214d61697
• 다음 코드는 35마리의 도미의 길이와 생선의 무게에 대한 데이터이다.

1
2
3
4
5
6

bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]      
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]

• 위 리스트에서 첫 번째 도미의 길이는 25.4cm, 무게는 242.0g이다.

• 각 도미의 특징을 길이와 무게로 표현했음을 알 수 있다.

• 책에서는 이런 특징을 특성(feature)이라 부른다.

• 길이인 bream_length를 x축으로 삼는다.

• 무게인 bream_weight를 y축으로 한다.

• 이를 토대로 각 도미를 그래프에 점으로 표시해 보자.

  • 이런 그래프를 산점도(scatter plot)라 부른다.

1
2
3
4
5
6

import matplotlib.pyplot as plt # matplotlib의 pyplot 함수를 plt로 줄여서 사용

plt.scatter(bream_length, bream_weight)
plt.xlabel('length')            # x 축은 길이
plt.ylabel('weight')            # y 축은 무게
plt.show()

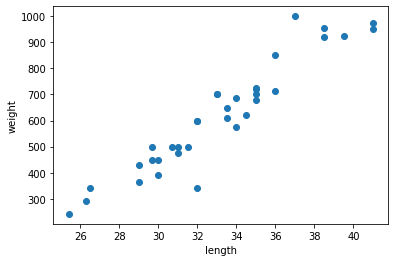
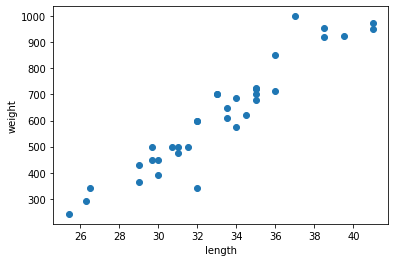
• 도미 35마리를 2차원 그래프에 점으로 나타냈다.
• 생선의 길이가 길수록 무게가 많이 나간다고 생각하면 이 그래프는 매우 자연스럽다.
• 이렇게 산점도 그래프가 일직선에 가까운 형태로 나타나는 경우를 선형적(linear)이라고 한다.

빙어 데이터 준비하기

• 이번엔 빙어의 데이터를 준비해 보자.
• 데이터는 다음 링크를 참고하라 : https://gist.github.com/rickiepark/1e89fe2a9d4ad92bc9f073163c9a37a7
• 다음 코드는 14 마리의 빙어에 대한 데이터이다.

1
2

smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

• 빙어는 도미에 비해 크기도 작고 무게도 가볍다.
• 빙어의 데이터도 산점도로 그려보자.
• 하는 김에 도미와 빙어의 산점도를 비교한다.

1
2
3
4
5

plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

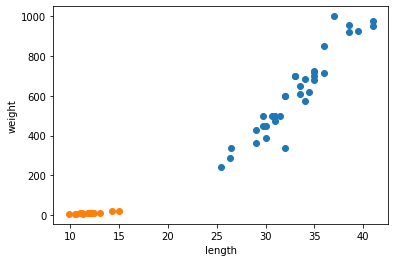
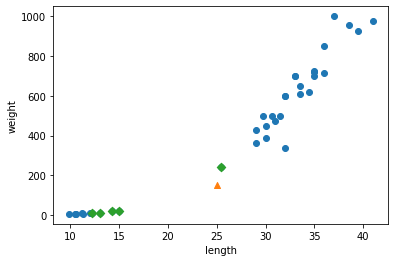
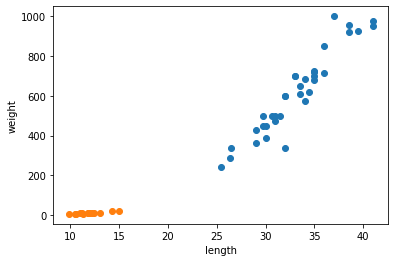
• Matplotlib에 의해 두 산점도 색깔이 다르게 출력된다.
• 주황색 점이 빙어의 산점도이며 도미에 비해 길이도 무게도 작다.
• 또한 빙어는 도미와 달리 길이가 늘어나도 무게가 크게 늘지 않는다는 것을 알 수 있다.

첫 번째 머신러닝 프로그램

• 가장 간단하고 이해하기 쉬운 k-최근접 이웃(k-Nearest Neighbors) 알고리즘을 사용해 도미와 비엉 데이터를 구분해본다.
• 알고리즘 사용 이전에 앞서 준비했던 두 생선의 데이터를 합친다.

1
2

length = bream_length + smelt_length
weight = bream_weight + smelt_weight

• 책에서 사용하는 머신러닝 패키지는 사이컷런(scikit-learn)이다.
• 이 패키지를 이용하여 각 특성의 리스트를 세로 방향으로 늘어뜨린 2차원 리스트를 만들어야 한다.
• 이렇게 만들기 위해서 파이썬의 zip() 함수와 리스트 내포(list comprehension)구문을 사용한다.
• zip() 함수는 나열된 리스트 각각에서 하나씩 원소를 꺼내 반환한다.
• zip() 함수와 리스트 내포 구문을 사용해 length와 weight 리스트를 2차원 리스트로 만들어보자.

1

fish_data = [[l, w] for l, w in zip(length, weight)]

• for문은 zip() 함수로 length와 weight 리스트에서 원소를 하나씩 꺼내어 l과 w에 할당한다.
• 그러면 [l, w] 가 하나의 원소로 구성된 리스트가 만들어진다.

1

print(fish_data)

[[25.4, 242.0], [26.3, 290.0], [26.5, 340.0], [29.0, 363.0], [29.0, 430.0], [29.7, 450.0], [29.7, 500.0], [30.0, 390.0], [30.0, 450.0], [30.7, 500.0], [31.0, 475.0], [31.0, 500.0], [31.5, 500.0], [32.0, 340.0], [32.0, 600.0], [32.0, 600.0], [33.0, 700.0], [33.0, 700.0], [33.5, 610.0], [33.5, 650.0], [34.0, 575.0], [34.0, 685.0], [34.5, 620.0], [35.0, 680.0], [35.0, 700.0], [35.0, 725.0], [35.0, 720.0], [36.0, 714.0], [36.0, 850.0], [37.0, 1000.0], [38.5, 920.0], [38.5, 955.0], [39.5, 925.0], [41.0, 975.0], [41.0, 950.0], [9.8, 6.7], [10.5, 7.5], [10.6, 7.0], [11.0, 9.7], [11.2, 9.8], [11.3, 8.7], [11.8, 10.0], [11.8, 9.9], [12.0, 9.8], [12.2, 12.2], [12.4, 13.4], [13.0, 12.2], [14.3, 19.7], [15.0, 19.9]]

• 2차원 리스트

  • 첫 번째 생선의 길이 25.4cm와 무게 242.0g이 하나의 리스트를 구성하고 이런 리스트가 모여 전체 리스트를 만들었다.
  • 이런 리스트를 2차원 리스트 혹은 리스트의 리스트라고 부른다.

• 생선 49개의 데이터가 준비되었다.

• 이제 마지막으로 준비할 데이터는 정답 데이터이다.

• 각 데이터가 실제로는 어떤 생선인지 정답지를 만드는 작업니다.

• 정답 리스트

  • 머신러닝은 물론이고 컴퓨터 프로그램은 문자를 직접 이해하지 못한다.
  • 대신 도미와 빙어를 숫자 1과 0으로 표현해보자
  • 앞서 도미와 방어를 순서대로 나열했기에 정답 리스트는 1이 35번 등장하고 0이 14번 등장한다.

1
2

fish_target = [1] * 35 + [0] * 14
print(fish_target)

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

• 이제 사이킷런 패키지에서 k-최근접 이웃 알고리즘을 구현한 클래스인 KNeighborsClassifier를 임포트한다.

1

from sklearn.neighbors import KNeighborsClassifier

• 임포트한 KNeighborsClassfier 클래스의 객체를 먼저 만든다.

1

kn = KNeighborsClassifier()

• 훈련
  • 이 객체에 fish_data와 fish_target을 전달하여 도미를 찾기 위한 기준을 학습시킨다.
  • 이런 과정을 머신러닝에서는 훈련(training)이라 부른다.
  • 사이킷런에서는 fit() 메서드가 이런 역할을 한다.
  • 이 메서드에 fish_data 와 fish_target 을 순서대로 전달해보자.

1

kn.fit(fish_data, fish_target)

KNeighborsClassifier()

• 평가
  • fit() 메서드는 주어진 데이터로 알고리즘을 훈련한다.
  • 이제 객체(또는 모델) kn이 얼마나 잘 훈련되었는지 평가해봐야 한다.
  • 사이킷런에서 모델을 평가하는 메서드는 score()메서드이다.
  • 이 메서드는 0에서 1 사이의 값을 반환한다.
  • 1은 모든 데이터를 정확히 맞혔다는 것을 나타낸다.
    • 예를 들어 0.5라면 절반만 맞혔다는 의미이다.

1

kn.score(fish_data, fish_target)

1.0

• 정확도
  • 1.0 이 출력되었다.
  • 모든 fish_data의 답을 정확히 맞혔다는 뜻이 된다.
  • 이러한 값을 정확도(accuracy)라고 부른다.

k-최근접 이웃 알고리즘

• 앞에서 첫 번째 머신러닝 프로그램을 성공적으로 만들었다.

• 여기에서 사용한 알고리즘은 k-최근접 이웃이다.

• 이 알고리즘은 어떤 데이터에 대한 답을 구할 때 주위의 다른 데이터를 보고 다수를 차지하는 것을 정답으로 사용하다.

  • 마치 근묵자흑과 같이 주위의 데이터로 현재 데이터를 판단하는 것이다.

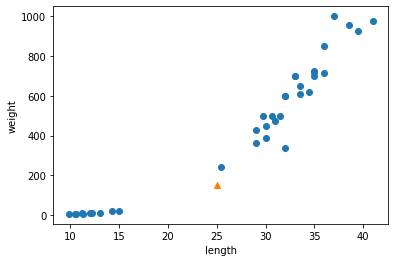
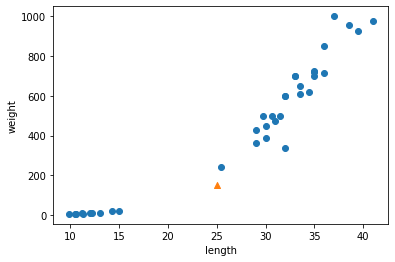
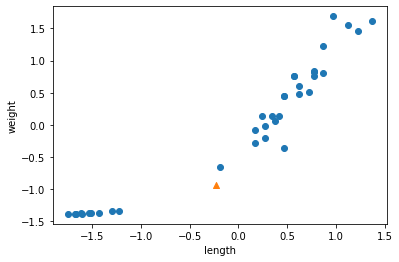
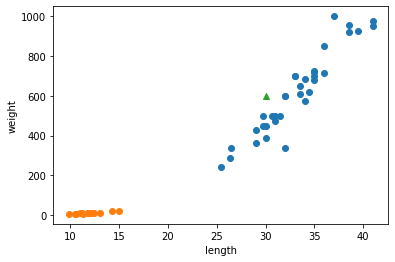
• 예를 들어, 이전에 출력한 산점도에서 삼각형으로 표시된 새로운 데이터가 있다고 가정해 보자.

• 이 삼각형은 도미와 빙어 중 어디에 속할까?

• 이 삼각형이 도미의 데이터 부근에 위치해 있다면 도미라고 판단할 것이다.

• k-최급접 이웃 알고리즘도 마찬가지이다.

• 실제 코드로도 그런지 한 번 확인해 보자.

1

kn.predict([[30, 600]])   # 2차원 리스트

array([1])

• predict() 메서드

  • predict() 메서드는 새로운 데이터의 정답을 예측한다.
  • 이 메서드도 앞서 fit() 메소드와 마찬가지로 2차원 리스트를 전달해야 한다.
  • 그래서 삼각형 포인트를 리스트로 2번 감싼것이다.
  • 반환되는 값은 1.
    • 우리는 앞서 도미는 1, 빙어는 0으로 가정했다.
    • 즉, 삼각형은 도미이다.

• k-최근접 이웃 알고리즘을 위해 준비해야 하는 것은 데이터를 모두 가지고 있는 것 뿐이다.

• 새로운 데이터에 대해 예측할 때는 가장 가까운 직선거리에 어떤 데이터가 있는지를 살피기만 하면 된다.

• 단점으로는 이런 특징 때문에 데이터가 아주 많은 경우 사용하기 어렵다는 점이 있다.

• 사이킷런의 KNeighborsClassifier 클래스도 마찬가지이다.

• 이 클래스는 _fit_X 속성에 우리가 전달한 fish_data를 모두 가지고 있다.

• 또 _y 속성에 fish_target을 가지고 있다.

1

print(kn._fit_X)

[[  25.4  242. ]
 [  26.3  290. ]
 [  26.5  340. ]
 [  29.   363. ]
 [  29.   430. ]
 [  29.7  450. ]
 [  29.7  500. ]
 [  30.   390. ]
 [  30.   450. ]
 [  30.7  500. ]
 [  31.   475. ]
 [  31.   500. ]
 [  31.5  500. ]
 [  32.   340. ]
 [  32.   600. ]
 [  32.   600. ]
 [  33.   700. ]
 [  33.   700. ]
 [  33.5  610. ]
 [  33.5  650. ]
 [  34.   575. ]
 [  34.   685. ]
 [  34.5  620. ]
 [  35.   680. ]
 [  35.   700. ]
 [  35.   725. ]
 [  35.   720. ]
 [  36.   714. ]
 [  36.   850. ]
 [  37.  1000. ]
 [  38.5  920. ]
 [  38.5  955. ]
 [  39.5  925. ]
 [  41.   975. ]
 [  41.   950. ]
 [   9.8    6.7]
 [  10.5    7.5]
 [  10.6    7. ]
 [  11.     9.7]
 [  11.2    9.8]
 [  11.3    8.7]
 [  11.8   10. ]
 [  11.8    9.9]
 [  12.     9.8]
 [  12.2   12.2]
 [  12.4   13.4]
 [  13.    12.2]
 [  14.3   19.7]
 [  15.    19.9]]

1

print(kn._y)

[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
 0 0 0 0 0 0 0 0 0 0 0 0]

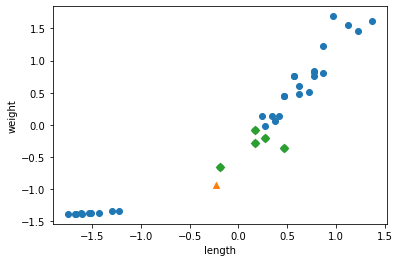
• 실제로 k-최근접 이웃 알고리즘은 무언가 훈련되는 게 없는 셈이다.
• fit()메서드에 전달한 데이터를 모두 저장하고 있다가 새로운 데이터가 등장하면 가장 가까운 데이터를 참고하여 어떤 생선인지 구분한다.
• 그럼 가까운 몇 개의 데이터를 참고할까?
  • 이는 정하기 나름이다.
  • KNeighborsClassifier 클래스의 기본값은 5이다.
  • 이 기준은 n_neighbors 매개변수로 바꿀 수 있다.
  • 예를 들어, 다음 코드 실행 시 어떤 결과가 나올까?

1

kn49 = KNeighborsClassifier(n_neighbors=49)     # 참고 데이터를 49개로 한 kn49 모델

• 가장 가까운 데이터 49개를 사용하는 k-최근접 이웃 모델에 fish_data를 적용하면 fish_data에 있는 모든 생선을 사용하여 예측하게 된다.
• 다시 말하면 fish_data의 데이터 49개 중에 도미가 35개로 다수를 차지하므로 어떤 데이터를 넣어도 무조건 도미로 예측할 것이다.

1
2

kn49.fit(fish_data, fish_target)
kn49.score(fish_data, fish_target)

0.7142857142857143

• fish_data에 있는 생선 중에 도미가 35개이고 빙어가 14개이다.
• kn49모델은 도미만 올바르게 맞히기 때운에 다음과 같이 정확도를 계산하면 score() 메서드와 같은 값을 얻을 수 있다.

1

print(35/49)

0.7142857142857143

• 확실히 n_neighbors 매개변수를 49로 두는 것은 좋지 않다.
• 기본 값을 5로 하여 도미를 완벽하게 분류한 모델을 사용하기로 한다.

도미와 빙어 분류 (중간 정리)

• 지금까지 도미와 빙어를 구분하기 위해 첫 머신러닝 프로그램을 만들었다.
• 먼저 도미 35마리와 빙어 14마리의 길이와 무게를 측정해서 파이썬 리스트로 만든다.
• 그 다음 도미와 빙어 데이터를 합친 2차원 리스트를 준비했다.
• 사용한 머신러닝 알고리즘은 k-최근접 이웃 알고리즘이다.
• 사이킷런의 k-최근접 이웃 알고리즘은 주변에서 가장 가까운 5개의 데이터를 보고 다수결의 원칙에 따라 데이터를 예측한다.
• 이 모델은 준비된 데이터를 모두 맞혔다.
• 도미와 빙어를 분류하는 문제를 풀면서 KNeighborsClassifier 클래스의 fit(), score(), predict() 메서드를 사용해 보았다.
• 끝으로 k-최근접 이웃 알고리즘의 특징을 알아보았다.

전체 소스 코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

# 마켓과 머신러닝
# 생선 분류 문제
# 도미 데이터 준비하기

bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]      
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]

import matplotlib.pyplot as plt # matplotlib의 pyplot 함수를 plt로 줄여서 사용

plt.scatter(bream_length, bream_weight)
plt.xlabel('length')            # x 축은 길이
plt.ylabel('weight')            # y 축은 무게
plt.show()

# 빙어 데이터 준비하기
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

# 첫 번째 머신러닝 프로그램

length = bream_length + smelt_length
weight = bream_weight + smelt_weight

fish_data = [[l, w] for l, w in zip(length, weight)]

print(fish_data)

fish_target = [1] * 35 + [0] * 14
print(fish_target)

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier()

kn.fit(fish_data, fish_target)

kn.score(fish_data, fish_target)

# k-최근접 이웃 알고리즘

plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.scatter(30, 600, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

kn.predict([[30, 600]])   # 2차원 리스트

print(kn._fit_X)

print(kn._y)

kn49 = KNeighborsClassifier(n_neighbors=49)     # 참고 데이터를 49개로 한 kn49 모델

kn49.fit(fish_data, fish_target)
kn49.score(fish_data, fish_target)

print(35/49)

[[25.4, 242.0], [26.3, 290.0], [26.5, 340.0], [29.0, 363.0], [29.0, 430.0], [29.7, 450.0], [29.7, 500.0], [30.0, 390.0], [30.0, 450.0], [30.7, 500.0], [31.0, 475.0], [31.0, 500.0], [31.5, 500.0], [32.0, 340.0], [32.0, 600.0], [32.0, 600.0], [33.0, 700.0], [33.0, 700.0], [33.5, 610.0], [33.5, 650.0], [34.0, 575.0], [34.0, 685.0], [34.5, 620.0], [35.0, 680.0], [35.0, 700.0], [35.0, 725.0], [35.0, 720.0], [36.0, 714.0], [36.0, 850.0], [37.0, 1000.0], [38.5, 920.0], [38.5, 955.0], [39.5, 925.0], [41.0, 975.0], [41.0, 950.0], [9.8, 6.7], [10.5, 7.5], [10.6, 7.0], [11.0, 9.7], [11.2, 9.8], [11.3, 8.7], [11.8, 10.0], [11.8, 9.9], [12.0, 9.8], [12.2, 12.2], [12.4, 13.4], [13.0, 12.2], [14.3, 19.7], [15.0, 19.9]]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

[[  25.4  242. ]
 [  26.3  290. ]
 [  26.5  340. ]
 [  29.   363. ]
 [  29.   430. ]
 [  29.7  450. ]
 [  29.7  500. ]
 [  30.   390. ]
 [  30.   450. ]
 [  30.7  500. ]
 [  31.   475. ]
 [  31.   500. ]
 [  31.5  500. ]
 [  32.   340. ]
 [  32.   600. ]
 [  32.   600. ]
 [  33.   700. ]
 [  33.   700. ]
 [  33.5  610. ]
 [  33.5  650. ]
 [  34.   575. ]
 [  34.   685. ]
 [  34.5  620. ]
 [  35.   680. ]
 [  35.   700. ]
 [  35.   725. ]
 [  35.   720. ]
 [  36.   714. ]
 [  36.   850. ]
 [  37.  1000. ]
 [  38.5  920. ]
 [  38.5  955. ]
 [  39.5  925. ]
 [  41.   975. ]
 [  41.   950. ]
 [   9.8    6.7]
 [  10.5    7.5]
 [  10.6    7. ]
 [  11.     9.7]
 [  11.2    9.8]
 [  11.3    8.7]
 [  11.8   10. ]
 [  11.8    9.9]
 [  12.     9.8]
 [  12.2   12.2]
 [  12.4   13.4]
 [  13.    12.2]
 [  14.3   19.7]
 [  15.    19.9]]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
 0 0 0 0 0 0 0 0 0 0 0 0]
0.7142857142857143

마무리

키워드로 끝내는 핵심 포인트

• 특성 : 데이터를 표현하는 하나의 성질.

  • 이 절에서 생선 데이터 각각을 길이와 무게 특성으로 나타냈다.

• 훈련 : 머신러닝 알고리즘이 데이터에서 규칙을 찾는 과정.

  • 사이킷런에서는 fit() 메서드가 하는 역할이다.

• k-최근접 이웃 알고리즘 : 가장 간단한 머신러닝 알고리즘 중 하나.

  • 사실 어떤 규칙을 찾기보다는 전체 데이터를 메모리에 가지고 있는 것이 전부이다.

• 모델 : 머신러닝 프로그램에서는 알고리즘이 구현된 객체를 모델이라 부른다.

  • 종종 알고리즘 자체를 모델이라고 부르기도 한다.

• 정확도 : 정확한 답을 몇 개 맞혔는지를 백분율로 나타낸 값이다.

  • 사이킷런에서는 0~1 사이의 값으로 출력된다.
  • 정확도 = (정확히 맞힌 개수) / (전체 데이터 개수)

핵심 패키지와 함수

• matplotlib

  • scatter()는 산점도를 그리는 Matplotlib 함수이다.
  • 처음 2개의 배개변수로 x축과 y축 값을 전달한다.
  • 이 값은 파이썬 리스트 또는 넘파이 배열이다.
  • c 매개변수로 색깔을 지정한다.

• scikit-learn

  • KneighborsClassifier()는 k-최근접 이웃 분류 모델을 만드는 사이킷런 클래스이다.
    • n_neighbors 매개변수로 이웃의 개수를 지정한다.
    • 기본값은 5이다.
    • p 매개변수로 거리를 재는 방법을 지정한다.
    • 1일 경우 맨해튼 거리(https://bit.ly/man_distance)를 사용한다.
    • 2일 경우 유클리디안 거리(https://bit.ly/euc_distance)를 사용한다.
    • 기본 값은 2이다.
  • fit()은 사이킷런 모델을 훈련할 때 사용하는 메서드이다.
    • 처음 두 매개변수로 훈련에 사용할 특성과 정답 데이터를 전달한다.
  • predict()는 사이킷런 모델을 훈련하고 예측할 때 사용하는 메서드이다.
    • 특성 데이터 하나만 매개변수로 받는다.
  • score()는 훈련된 사이킷런 모델의 성능을 측정한다.
    • 처음 두 매개변수로 특성과 정답 데이터를 전달한다.
    • 이 매서드는 먼저 predict() 메서드로 예측을 수행한 다음 분류 모델일 경우 정답과 비교해 맞게 예측한 개수의 비율을 반환한다.

확인 문제

1. 데이터를 표현하는 하나의 성질로써, 예를 들어 국가 데이터의 경우 인구 수, GDP, 면적 등이 하나의 국가를 나타냅니다. 머신러닝에서 이런 성질을 무엇이라 부르나요?

• 1. 특성 v
• 2. 특질
• 3. 개성
• 4. 요소

2. 가장 가까운 이웃을 참고하여 정답을 예측하는 알고리즘이 구현된 사이킷런 클래스는 무엇인가요?

• 1. SGDClassifier
• 2. LinearRegression
• 3. RandomForestClassifier
• 4. KNeighborsClassifier v

3. 사이킷런 모델을 훈련할 때 사용하는 메서드는 어떤 것인가요?

• 1. predict()
• 2. fit() v
• 3. score()
• 4. transform()

• Reference : 혼자 공부하는 머신러닝 + 딥러닝